Forças / Palestra

Força

Em física clássica, a força (F) é aquilo que pode alterar (num mesmo referencial assumido inercial) o estado de repouso ou de movimento de um corpo, ou de deformá-lo. Esta definição não pode ser desvinculada da Terceira Lei de Newton (que "afirma" que a força é a expressão física para a interação entre dois entes físicos [ou entre duas partes de um mesmo ente], definindo então a direção, o sentido e a igualdade dos módulos das forças de um par ação-reação), e da Segunda Lei de Newton (que define o módulo da força baseando-se na definição de aceleração e do quilograma-padrão [massa]). Pode-se definir força, sucintamente, como a causa de qualquer modificação no estado de um corpo, podendo causar sua deformação ou alteração do estado de movimento, tirando o corpo do repouso ou do movimento retilíneo uniforme. A força também pode causar deformação e movimento de uma só vez.

Detectamos uma força através de seus efeitos e suas consequências. Estes podem ser: a variação no módulo da velocidade do corpo (por exemplo, quando se dá um chute numa bola que se encontrava em repouso); uma alteração na direcção e sentido do movimento do corpo (noMovimento Circular Uniforme ou no "efeito" no voo de uma bola); ou pode haver uma deformação no corpo em que é aplicada a força (e.g. a deformação momentânea da bola quando é chutada).

Fórmula da força

Para um corpo de massa constante, a força resultante sobre ele possui módulo igual ao produto entremassa e aceleração

.

Tal equação provém da segunda Lei de Newton ou princípio fundamental da dinâmica (p.f.d.).

---

De maneira mais geral temos que força é a derivada temporal total do momento linear ou quantidade de movimento . Para o caso de massa constante, esta mostra-se análoga à primeira.

As três leis de Newton

Isaac Newton, a partir de suas reflexões e análises, enunciou as três leis básicas do movimento que herdaram o seu nome, em homenagem.

Primeira Lei de Newton

Esta lei responde à pergunta sobre o que é Referencial inercial, e remove a ideia aristotélica de que é necessária a presença de uma força para que um corpo permaneça em movimento. As definições deInércia e de referencial inercial fundamentam-se na ideia de força conforme definido (como a expressão física da interação entre DOIS entes físicos), e assim o conceito de força é primordial dentro das leis da mecânica.

Segunda Lei de Newton

Esta lei pode ser assim enunciada: a força que atua em um corpo é diretamente proporcional à aceleração que ele apresenta, e a constante de proporcionalidade é a massa do corpo. Repare que a Segunda Lei completa (baseada na Terceira Lei e na Primeira Lei) é a definição de força, estabelecendo ela o módulo e também a unidade desta. A unidade de força deriva de unidades pré-estabelecidas: a unidade de aceleração (m/s²) e a de massa (Kg - vide quilograma-padrão).

Quando uma força é aplicada, esta produz trabalho e transfere ou remove energia do objeto sobre o qual atua, desde que o objeto se mova de forma paralela à força aplicada.

As pseudo-forças ou forças inerciais "transformam", imaginariamente, um referencial não inercial em inercial, permitindo que as previsões decorrentes do uso das Leis de Newton nas referências não inerciais concordem com o que é observado a partir destes referenciais. Sem estas correções, as previsões e as observações não concordariam. O nome força inercial dado às estas pseudo-forças é portanto bem sugestivo.

Terceira Lei de Newton

Esta lei refere-se à força como expressão física da interação entre DOIS objetos. Segundo esta Lei, para haver força, ou melhor: forças (uma vez que sempre aparecem aos pares), devemos ser capaz de encontrar DOIS físicos em interação. Se não formos capazes de identificar os dois objetos ou entes, e acharmos que existe uma força sobre um único objeto do universo, então estaremos diante do que se chama em física de pseudo-força (falsa força) ou força inercial, e não de uma força em sua definição formal. O exemplo mais preciso é o do movimento circular, onde há uma força centrípeta(real), mas não há uma força (na definição do termo) centrífuga. A força centrífuga não existe como força real e sim como uma pseudo-força (uma falsa força) observada em referenciais NÃO inerciais.

A Terceira Lei pode ser assim enunciada: se um corpo "A" aplicar uma força sobre um corpo "B", este último aplicará sobre "A" outra força da mesma intensidade e mesma direção, mas no sentido contrário.

Forças fundamentais

Da interação entre entes físicos

Na natureza reconhecemos quatro tipos de forças fundamentais, enumeradas por sua ordem de grandeza:

A força nuclear forte e a força nuclear fraca estão presentes no núcleo atômico e não são observadas no cotidiano.

A força eletromagnética é responsável por todas as interações observadas no dia-a-dia, excetuando-se as interações gravitacionais.

A força da gravidade constitui-se na quarta espécie de força, sobre a qual Newton se debruçou, questionando-se sobre o motivo dos objectos caírem no solo (fábula da maçã caindo junto ao nascer da lua no horizonte).

Galileu já tinha descoberto que os objetos aceleravam à medida que caíam, (ou seja, que sofriam alterações no seu movimento), e que os corpos próximos à superfície terrestre caem (em queda livre) com a mesma aceleração: a aceleração da gravidade. Newton justificou este fato "definindo" e descrevendo o comportamento de uma força que um corpo massivo exerce sobre outro corpo massivo: a força da gravidade. Os objetos próximos à Terra caem devido à força de atração gravitacional entre a Terra (com sua enorme massa) e o objeto (com massa diminuta). Pelo mesmo motivo, os objetos celestes são mantidos em suas órbitas uns ao redor dos outros (Por exemplo: a Terra ao redor do Sol, e a Lua ao redor da Terra).

A lei da gravidade

A lei da gravidade de Newton é conhecida como Lei da Gravitação Universal, e com ela Newton "explicou" a atração gravitacional, e mostrou que diferente dos pensamentos herdados da sociedade grega antiga, a física celeste não era necessariamente diferente da física do mundo sublunar, e que em ambos os casos valia a Lei da Gravitação Universal e as demais leis.

Em homenagem, a unidade SI de força é o newton (N).

Considerando que a aceleração da gravidade terrestre próxima à superfície é um número próximo de 10 m/s²(embora por vezes apareça como 9,8m/s²), o peso de um corpo de 1.000 g (1 kg) aproxima-se de 10 N, ou seja: 1 kgf (quilograma força) = 9,8 N (newtons).

Definição avançada de força

O quilograma-padrão. Relação de dispersão para uma partícula clássica. Em todos os modelos dinâmicos o momento P e a energia E são definidos de forma a satisfazerem leis gerais de conservação.

Os conceitos físicos de força e massa surgem em teorias ou modelos destinados a estabelecer a dinâmica em sistemas compostos ou por entes semelhantes ou por entes de natureza às vezes bem distintas. Nestes modelos sempre figuram também dois outros conceitos fundamentais, o conceito de momento e o conceito de energia. Os conceitos de energia e momento são importantes porque suas definições se dão de forma que energia e momento sempre obedeçam a leis gerais de conservação, leis estas decorrentes da existência de regras naturais de relacionamento entre entes e/ou sistemas que são, em princípio, estáveis e muito bem estabelecidas. Neste contexto, energia e momento guardam íntima relação, e um ente físico é caracterizado pela sua relação de dispersão, um gráfico ou função que explicita a relação existente entre o momento e a energia para este ente.

É com base na definição de momento que se estabelece a definição geral de força nas teorias para a dinâmica de entes físicos:

- a força que atua em um ente corresponde à derivada de seu momento em relação ao tempo.

A expressão para a força dentro da mecânica newtoniana decorre diretamente da expressão 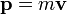para o momento 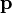, e iguala-se à conhecida expressão quando a massa é constante.

A expressão para a força dentro de uma teoria dinâmica mais avançada pode mostrar-se, entretanto, bem mais "complicada". Na relatividade restrita, onde o momento relativístico P é definido por:

a expressão derivada para a força é:

Esta expressão, bem diferente da equação fundamental da dinâmica, nos informa que, em relatividade, força e aceleração não são necessariamente paralelas. Há uma componente da força na direção da aceleração, mas há também uma componente da força na direção da velocidade da partícula. A compreensão da dinâmica quando se trata de relatividade requer assim uma intuição muito maior, geralmente fugindo da visão de mundo associada à mecânica newtoniana em nível comparável ao da mecânica de Aristóteles quando confrontada com a de Newton.

Na oportunidade cita-se, de passagem, a definição geral de massa:

- a massa de um dado ente físico corresponde ao inverso da derivada segunda da energia em relação ao momento.

Resumo final

Força

A força é a expressão vetorial e completa da interação entre dois entes físicos.

É definida, de forma geral, como a derivada temporal do momento: .

No escopo da Mecânica Clássica esta definição está derivada das três leis da dinâmica (Leis de Newton), e portanto sempre está de acordo com elas. As forças aparecem aos pares, sempre havendo para cada ação uma reação identificável.

Pseudo-força

As pseudo-forças (ou forças inerciais) são forças fictícias (não reais) utilizadas para "transformar" referenciais não inerciais em inerciais. As forças inerciais são acrescentadas aos cálculos para permitir o emprego das Leis de Newton e a descrição dos movimentos quando são vistos e descritos a partir de referenciais não inerciais. Não se consegue estabelecer um par ação-reação para uma força inercial. São (pseudo)forças solitárias. São exemplos a força centrífuga e a força de Coriolis.

Forças fundamentais

Há quatro formas de interação básicas entre dois entes físicos: a nuclear forte, a nuclear fraca, a eletromagnética e a gravitacional.

Excetuando-se a força da gravidade, toda interação observada no dia-a-dia tem natureza eletromagnética (incluindo-se a força de atrito e de contato).

A força da gravidade representa a interação entre dois objetos em virtude de suas massas (de repouso), e portanto afeta todos os objetos que existem na superfície da Terra, e também no universo. A força de gravidade é o peso.

Na Terra, a aceleração da gravidade vale aproximadamente g=9,8 m/s² , e o peso dos objetos pode ser calculado por . A força de reação do peso de qualquer objeto em relação à Terra está sempre na própria Terra.

Palestra

Bom eu achei a palestra muito interessante. Aprendi coisas que eu nem sabia, conheci coisas novas. Foi muito legal, pois com as instruções que o agentes da saúde deram, me ajudou a ter noção do que é fazer uma relação com proteção. Sem o risco de pegar doenças entre outras coisas, e também me ajudou em várias dúvidas que eu tinha sobre esse assunto.

Thobias Estanislau - 2001